Dynamic programming: a compelling case for arrays

The array is perhaps the first data structure that many individuals are exposed to. The two dimensional array is extremely common - any board game that uses a grid exercises the idea. The number of examples are nearly endless - checkers, chess… endless.

Let’s start from ground zero. What is an array? It’s a particular arrangement, in one or more dimensions, of a bunch of the same type of objects. Probably the most important charactestic of this arrangement is that it provides O(1) lookup (i.e. fast retrieval of the ith element, for any i).

The simplest array might be this one, in one dimension:

One of the most timeless homes of the array is perhaps dynamic programming. Computing terms of the Fibonacci sequence is such a good problem for motivating dynamic programming, that we should take a minute right now¹ to check it out.

First of all - we need to understand the definition of the sequence:

(F_i means the ith term of the sequence.)

Let F_0 = 0, F_1 = 1, and F_n = F_n-1 + F_n-1.

In other words, every term is the sum of the previous two terms, starting from the terms 0 and 1.

A natural first take would be recursive, like the solution below in Python.

def fibonacci(n):
"""
Returns the nth term of he Fibonacci sequence.
"""
if n <= 1:
    return 1
else:
    return fibonacci(n - 1) + fibonacci(n - 2)

Surely, the solution is elegant, concise, easy to read and verify, etc. Basically everything you want in a function. What it isn’t is a model of efficiency.

(For the functools savvy - let’s ignore the existence of the lrucache decorator for the sake of discussion).

Imagine the required computations in a graph - specifically, a binary tree. Each term requires computing the two terms prior to it. The maximum depth of the tree will be n (the longest path consists of the one where the immediately preceding term is calculated each time). How many nodes are in a full binary tree with depth n? It’s 2^n nodes. Yikes. Even if that’s just an unrefined upper bound, it’s terrible for even moderate values of n.

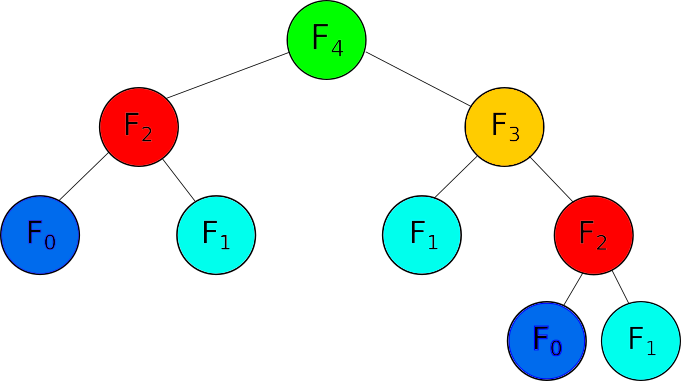
Our first observation is that the same calculations are repeated many, many times (the colored highlights in the image above show repetition in the relatively benign case of computing the 4th term). How do we avoid this trap?

What we can do is recognize that the solution can be built, one term at a time, in O(n) time. That is, starting with the first two terms, compute the next term, until the desired term is reached.

And this is where the array comes in. We need a good way to access the previous two numbers. (I want to take a second to mention that a list would do just as well as an array here. We really only need O(1) lookup of the two previous nodes and O(1) adding of an element to the end. A pre-sized² array will do nicely, as would a linked list.)

The image below is what the constructed array would look like for the same 4th term. Note that each required term in the sequence is only computed once. I’ve also taken the liberty to swap to the actual values of the sequence.

In the simplest sense - that’s dynamic programming. The gist is to break large problems down into subproblems such that you can populate a “lookup table” of answers to those subproblems. To solve the big problem, build up the solution from a library of smaller solutions. This can eliminate a lot of redundant operations compared to brute force.

The real art is figuring out how to decompose problems into a sensible structure of subproblems (and their combination to form other solutions). Something like the change-making problem would be good to explore as a next step.

With these more complicated instances of dynamic programming - requiring more sophisticated lookup in arrays of increasing dimensions and size, the qualities of the array become indispensible.